Question

A man standing 1.54 m in front of a shaving mirror produces a real, inverted image 15.2 cm from it. What is the focal length of the mirror? (b) How close to the mirror should he stand if he wants to form an upright image of his chin that is twice the chin's actual size?

Answer 1

The focal length is 16.86 cm and the distance of the man if he wants to form an upright image of his chin that is twice the chin's actual size is 8.43 cm.

Step-by-step explanation:

Given that,

Object distance u=1.54 m =154 cm

Image distance v = 15.2 cm

Magnification = 2

We need to calculate the focal length

Using formula of mirror

`(1)/(f)=(1)/(v)+(1)/(u)`

Put the value into the formula

`(1)/(f)=(1)/(15.2)+(1)/(-154)`

`(1)/(f)=(347)/(5852)`

`f=16.86\ cm`

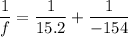
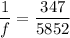
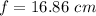
We need to calculate the focal length

Using formula of magnification

`m= (-v)/(u)`

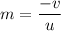
Put the value into the formula

`2=(v)/(u)`

`v = -2u`

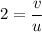
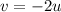
Using formula of for focal length

`(1)/(f)=(1)/(u)+(1)/(v)`

`(1)/(16.86)=(1)/(u)-(1)/(2u)`

`(1)/(16.86)=(1)/(2u)`

`2u=16.86`

`u=(16.86)/(2)`

`u=8.43\ cm`

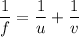
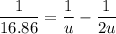
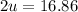
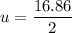
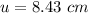
Hence, The focal length is 16.86 cm and the distance of the man if he wants to form an upright image of his chin that is twice the chin's actual size is 8.43 cm.