Question

1 Point

What is the graph of the solution to the following compound inequality?
5x-1 < 19 and -3 - x+1 <1
A
B
C
D

Answer 1

The correct graph of the solution to the given compound inequality is:

C

Explanation:

• The first inequality is given by:

`5x-1<19`

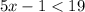
on adding 1 on both the side of the inequality we have:

`5x<20`

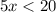
on dividing both side of the inequality by 5 we have:

`x<(20)/(5)\\\\x<4`

The graph of this inequality is the shaded region to the left of 4 with a open circle at 4( since the inequality is strict)

• The second inequality is:

`-3-x+1\leq 1\\\\-3+1-x\leq 1\\\\-2-x\leq 1\\\\-2-1\leq x\\\\x\geq -3`

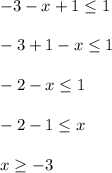
The graph of this inequality is the shaded region to the right of -3 and closed circle at -3 ( since the inequality is not strict i.e. a inequality with a equality sign )

Hence, the graph of the compound inequality is the set of all the points between -3 and 4 including -3 and excluding 4.

Answer 2

Option C

Explanation:

The given inequality is

5x-1 < 19 and
`-3-x+1\le1`

Group similar terms to get:

5x < 19+1 and
`-x\le1-1+3`

5x < 20 and
`-x\le3`

Solve for x to get:

x < 4 and
`x\ge -3`

The correct choice is C