Answer:
inductance is 1.31 µH
capacitance is 1.658 pF
Step-by-step explanation:
Given data
frequency = 87.7 MHz = 87.7 ×
 Hz
Hz
capacitor = 2.50 pF = 2.50 ×
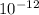 F
F
to find out
inductance and capacitance at 108 MHz
solution
we apply here resonant frequency that is
frequency = 1 / 2π√(LC) ..............1
here L is inductance and C is capacitor
put all the value and find L
√(L2.50 ×
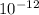 ) = 1 / 2π ( 87.7 ×
) = 1 / 2π ( 87.7 ×
 )
)
√(L2.50 ×
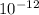 ) = 1.81 ×
) = 1.81 ×
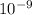
(L2.50 ×
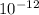 ) = 3.296 ×
) = 3.296 ×
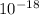
L = 3.296 ×
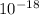 / 2.50 ×
/ 2.50 ×
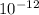
L = 1.31 ×
 H
H
so inductance is 1.31 µH
and
for 108 MHz = 108 ×
 Hz
Hz
we find here capacitance c from equation 1
frequency = 1 / 2π√(LC)
√(LC) =1 / 2π frequency
√(1.31 ×
 C) =1 / 2π ( 108 ×
C) =1 / 2π ( 108 ×
 )
)
√(1.31 ×
 C) = 1.47 ×
C) = 1.47 ×
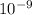
(1.31 ×
 C) = 2.178 ×
C) = 2.178 ×
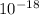
c = 2.178 ×
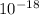 / (1.31 ×
/ (1.31 ×
 )
)
c = 1.658 ×
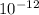 F
F
so capacitance is 1.658 pF