Question

An electron is accelerated from rest through a potential difference of 4.55 kV. It enters a region where a uniform 4.4-mT magnetic field is perpendicular to the velocity of the electron. Calculate the radius of the path this electron will follow in the magnetic field. (E = 1.60 x 10^-19 C, mass electron = 9.11 x 10^-31 kg)

Answer 1

Radius, r = 0.051 meters

Step-by-step explanation:

It is given that,

Potential difference,
`V=4.55\ kV=4.55* 10^3\ V`

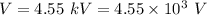
Magnetic field,
`B=4.4\ mT=4.4* 10^(-3)\ T`

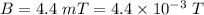
The magnetic field is perpendicular to the velocity of the electron. We need to calculate the radius of the path this electron will follow in the magnetic field.

The magnetic force is balanced by the centripetal force as:

`(mv^2)/(r)=qvB`

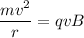
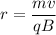`r=(mv)/(qB)`..........(1)

Using the conservation of energy as :

`(1)/(2)mv^2=eV`

`v=\sqrt{(2eV)/(m)}`

`v=\sqrt{(2* 1.6* 10^(-19)* 4.55* 10^3)/(9.1* 10^(-31))}`

`v=4* 10^7\ m/s`

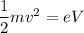
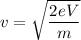
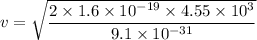
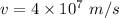
Equation (1) becomes :

`r=(9.1* 10^(-31)* 4* 10^7)/(1.6* 10^(-19)* 4.4* 10^(-3))`

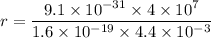
r = 0.051 m

So, the radius of the path this electron will follow in the magnetic field is 0.051 meters. Hence, this is the required solution.