Question

Calculate the distance traveled by a projectile as a function of launch angle. Compare the distances for two projectiles launched at the same initial velocity for two different launch angles. Discuss the case where the ranges are the same.

Answer 1

`R = x_(max) = (v^2\sin(2\theta))/(g)\\(R_1)/(R_2) = (\sin(2\theta_1)/(\sin(2\theta_2)`

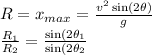
Step-by-step explanation:

Using kinematics equations:

`\Delta x = v_(0x)t\\\Delta y = -(1)/(2)gt^2+v_(0y)t`

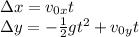
Use
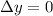`\Delta y = 0` due to condition of distance traveled.

Solving second equation for time, there are two solutions. t=0 and

`t=(2v_(0y))/(g)`

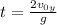
Use the expression in the first equation to have

`R = (2v^2 \cos\theta\sin\theta)/(g)`

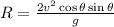
Using trigonometric identities, you have the answer of the distance.

By doing the ratio for two different angles, you have the second answer. Due to sine function properties, the distances can be the same to complementary angles. Example, for 20° and 70°, the distance is the same.