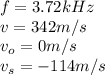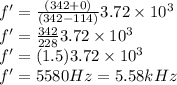Answer:
f'=5.58kHz
Step-by-step explanation:
This is an example of the Doppler effect, the formula is:
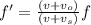
Where f is the actual frequency,
 is the observed frequency,
is the observed frequency,
 is the velocity of the sound waves,
is the velocity of the sound waves,
 the velocity of the observer (which is negative if the observer is moving away from the source) and
the velocity of the observer (which is negative if the observer is moving away from the source) and
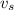 the velocity of the source (which is negative if is moving towards the observer). For this problem:
the velocity of the source (which is negative if is moving towards the observer). For this problem: