Answer:
energy is 36 mJ
radiation pressure exerted by the beam is 1.9254 ×
 Pa
Pa
Step-by-step explanation:
Given data
diameter = 2.3 mm = 2.3 ×
 m
m
power = 2.4 mW = 2.4 ×
 J/s
J/s
time = 15 s
to find out
energy and radiation pressure exerted
solution
we know for energy
that is energy = power × time
energy = 2.4 ×
 × 15
× 15
energy = 36 ×
 J
J
so energy is 36 mJ
and
now first we find cross section area that i s
cross section Area A = πd²/4
A = π(2.3 ×
 )²/4
)²/4
A = 4.155 ×
 m²
m²
and intensity of radiation will be power / area
so intensity of radiation = 2.4 ×
 / 4.155 ×
/ 4.155 ×

intensity of radiation = 577.62 W/m²
so that now for radiation pressure for beam that is
pressure = intensity of radiation / speed of light
we know speed of light is 3 ×
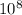 m/s
m/s
so
pressure = 577.62 / 3 ×
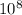
pressure = 1.9254 ×
 Pa
Pa
so radiation pressure exerted by the beam is 1.9254 ×
 Pa
Pa