Answer:
The correct answer is A : Orientation dependence of normal and shear stresses at a point in mechanical members
Step-by-step explanation:
Since we know that in a general element of any loaded object the normal and shearing stresses vary in the whole body which can be mathematically represented as
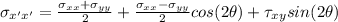
And
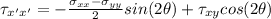
Mohr's circle is the graphical representation of the variation represented by the above 2 formulae in the general oriented element of a body that is under stresses.
The Mohr circle is graphically displayed in the attached figure.