Question

A researcher wishes to conduct a study of the color preferences of new car buyers. Suppose that 50% of this population prefers the color green. If 16 buyers are randomly selected, what is the probability that exactly 10 buyers would prefer green

Answer 1

`P(X=10) = 0.1222`

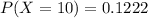
Explanation:

Represent Green with G

So,

`G = 50\%`

Required

Determine the probability that 10 out of 16 prefer green

This question is an illustration of binomial distribution and will be solved using the following binomial distribution formula.

`P(X=x) = ^nC_xG^x(1-G)^(n-x)`

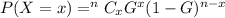
In this case:

`n = 16` -- number of people

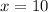`x = 10` -- those that prefer green

So, the expression becomes:

`P(X=10) = ^(16)C_(10)G^(10)(1-G)^(16-10)`

`P(X=10) = ^(16)C_(10)G^(10)(1-G)^(6)`

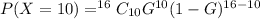
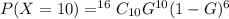
Substitute 50% for G (Express as decimal)

`P(X=10) = ^(16)C_(10)*0.50^(10)*(1-0.50)^(6)`

`P(X=10) = ^(16)C_(10)*0.50^(10)*0.50^(6)`

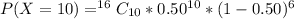
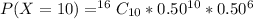
Apply law of indices

`P(X=10) = ^(16)C_(10)*0.50^{10+6`

`P(X=10) = ^(16)C_(10)*0.50^{16`

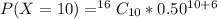
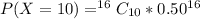
Solve 16C10

`P(X=10) = (16!)/((16-10)!10!) *0.50^{16`

`P(X=10) = (16!)/(6!10!) *0.50^{16`

`P(X=10) = (16*15*14*13*12*11*10!)/(6!10!) *0.50^{16`

`P(X=10) = (16*15*14*13*12*11)/(6!) *0.50^{16`

`P(X=10) = (16*15*14*13*12*11)/(6*5*4*3*2*1) * 0.50^{16`

`P(X=10) = (5765760)/(720) * 0.50^{16`

`P(X=10) = 8008 * 0.50^{16`

`P(X=10) = 8008 * 0.00001525878`

`P(X=10) = 0.12219231024`

`P(X=10) = 0.1222`

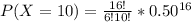
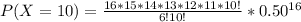
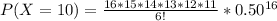
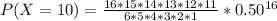
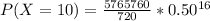
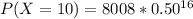
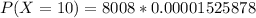
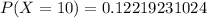
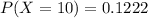
Hence, the required probability is 0.1222