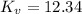Answer:
Step-by-step explanation:
Given;
For orifice, loss coefficient, K₀ = 10
Diameter, D₀ = 45 mm = 0.045 m
loss coefficient of the orifice, Ko = 10
Diameter of the gate valve, Dy = 1.5D₀ = 1.5 × 0.045 m = 0.0675 m
Total head drop, Δhtotal=25 m
Discharge, Q = 10 l/s = 0.01 m³/s
Now,
the velocity of flow through orifice, Vo = Discharge / area of the orifice
or
Vo =

or
Vo = 6.28 m/s
also,
the velocity of flow through gate valve,
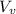 = Discharge / area of the orifice
= Discharge / area of the orifice
or
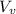 =
=
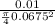
or
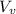 = 2.79 m/s
= 2.79 m/s
Now,
the total head drop = head drop at orifice + head drop at gate valve
or
25 m =
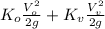
where,
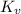 is the loss coefficient for the gate valve
is the loss coefficient for the gate valve
on substituting the values, we get
25 m =

or
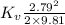 = 4.898
= 4.898
or