Answer:
XY = 18.6 mts
Angle of Depression = 61°
Explanation:
Let us start with finding out the Length of the XY
Y is directly on top of the center of the rectangular pool ABCD . Hence It must be on the top of the intersection point of the two diagonals. The length of XY will be half of Diagonal D .
Let us find Diagonal D by applying Pythagoras theorem in Triangle ABC
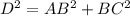
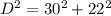
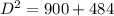
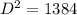
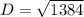
 Approx
Approx
Hence Diagonal is 37.20 mts
Hence

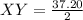
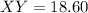 mts
mts
Hence we have our first answer as 18.6 Mts
Part 2:
Please refer to the image attached with this answer.
The eye of the diver , the eye of the man standing on the pool , and the diagonal of the pool makes a right triangle A'O'Y'
Where
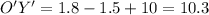
A'O' = half of the diagonal = 18.60 ( From first part of the problem)
Hence in ΔA'O'Y' , we have to determine ∠A'Y'O' or ∠x
Here applying trigonometric ratios
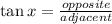
Opposite = A'O' = 18.60
Adjacent = Y'O' = 10.3
Hence
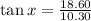
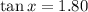

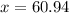
x≈61°
Hence Angle of depression for the diver towards the man standing at the pool edge would be 61°