Question

The Johnson twins were born five years after their older sister. This​ year, the product of the three​ siblings' ages is exactly 2998 more than the sum of their ages. How old are the​ twins?

Answer 1

13 years

Explanation:

Let x years be the age of each twins this year, then x+5 years is the age of their older sister this year.

The product of the ages of three sibling is

`x\cdot x\cdot (x+5)=x^3 +5x^2`

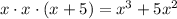
The sum of their ages is

`x+x+x+5=3x+5`

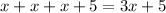
Since the product of the three​ siblings' ages is exactly 2998 more than the sum of their ages, we have

`x^3 +5x^2-(3x+5)=2,998\\ \\x^3 +5x^2-3x-5-2,998=0\\ \\x^3+5x^2-3x-3,003=0`

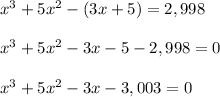
The divisors of 3,003 are

`\pm 1, \pm 3,\pm 7, \pm 11,\pm 13, \pm 21, \pm 33,\pm 77,....` and so on.

Check positive (the age cannot be negative) numbers to be equation's solutions:

`13^3+5\cdot 13^2-3\cdot 13-3,003=2,197+845-39-3,003=0`

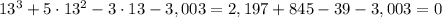
So,

`x^3+5x^2-3x-3,003=(x-13)(x^2+18x+231)=0`

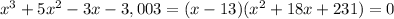
The quadratic equation has no real solutions, because its discriminant

`D=18^2-4\cdot 231=324-924=-600<0`

So, the twins are 13 years old (and the sister is 18 years old)