Answer:
They are collinear
Explanation:
Three or more points are collinear if and only if they lie on the same line. First of all, lets's plot these points. By using graph tools we get the first graph shown below. Seemingly they are collinear, but we have to prove this mathematically. To do so, let's use the distance formula:
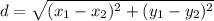
Let's rename the points as:
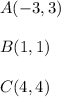
Hence, it must be true that:
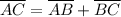
Therefore:
![\overline{AC}=√([4-(-3)]^2+[4-(-3)]^2) \\ \\ \overline{AC}=√((7)^2+(7)^2) \\ \\ \overline{AC}=√(49+49) \\ \\ \overline{AC}=√(98) \\ \\ \boxed{\overline{AC}=7√(2)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sstj4erw9kbd7k32m0odnqxg70ngx7m8nj.png)
![\overline{AB}=√([1-(-3)]^2+[1-(-3)]^2) \\ \\ \overline{AB}=√((4)^2+(4)^2) \\ \\ \overline{AB}=√(16+16) \\ \\ \overline{AB}=√(32) \\ \\ \boxed{\overline{AB}=4√(2)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6xjav5tiru98tt4kl1gbke494uodezbr16.png)
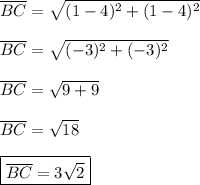
Then:
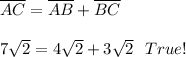
Given that
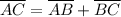 , then these three points are collinear.
, then these three points are collinear.