Question

Let $f(x)$ be a quartic polynomial with integer coefficients and four integer roots. Suppose the constant term of $f(x)$ is $6$.(a) Is it possible for $x=3$ to be a root of $f(x)$?(b) Is it possible for $x=3$ to be a double root of $f(x)$?2

Answer 1

By the rational root theorem, the answer to (a) is yes, and the answer to (b) is no. This is because 3 divides 6, but 3^2 = 9 does not divide 6.

Answer 2

It is given that, f(x) is a quartic polynomial with integer coefficients and four integer roots.

Constant Term of f(x)=6

(a)

By rational root theorem , the roots of the polynomial can be

`\pm 1,\pm 2,\pm 3,\pm 6`

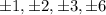
So, Yes x=3, can be root of f(x).

(b)

Yes, a quartic Polynomial , can have double root as x=3, that is two roots equal to , x=3.

For example,Consider the Polynomial

`\rightarrow (x^2-9)(x^2-(6)/(9))=0\\\\\rightarrow x^4-(6x^2)/(9)-9x^2+6=0\\\\\rightarrow x^4-(87x^2)/(9)+6=0`

has two zeroes equal to 3.