Step-by-step explanation:
It is given that,
Frequency of the siren, f = 2450 Hz
The speed of sound, v = 343 m/s
Here, both ambulance and the observer is stationary. The observed frequency is calculated using Doppler's effect as :

 is the velocity of observer
is the velocity of observer
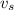 is the velocity of source
is the velocity of source
v is the speed of sound wave
Here,
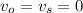
So, f' = f
f' = 2450 Hz
Wavelength,
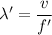

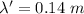
So, the frequency and wavelength of the observed sound is 2450 Hz and 0.14 meters. Hence, this is the required solution.