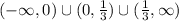Question

Determine the domain of the function (fog) (x) where f(x) = 3x-1/x-4 and g(x)=x+1/x

Answer 1

`(-\infty,0)\cup(0, (1)/(3))\cup ((1)/(3),\infty)`

Explanation:

The given functions are
`f(x)=(3x-1)/(x-4)` and
`g(x)=(x+1)/(x)` .

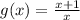We now composed the two functions to find:

`(f\circ g)(x)=f(g(x))`

`\implies (f\circ g)(x)=f((x+1)/(x))`

`\implies (f\circ g)(x)=(3((x+1)/(x))+1)/((x+1)/(x)-4)`

`\implies (f\circ g)(x)=(4x+3)/(1-3x)`

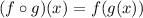
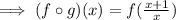
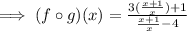
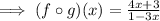
This function is defined if the denominator is not zero.

`1-3x\\e0`

`x\\e(1)/(3)`

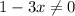
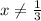
We write this in interval notation as:

`(-\infty,(1)/(3))\cup ((1)/(3),\infty)`

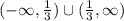
We need to be cautious here as x=0 is not in the domain of g(x).

Therefore the domain of
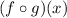`(f\circ g)(x)` is

`(-\infty,0)\cup(0, (1)/(3))\cup ((1)/(3),\infty)`