Question

The only items in a container A are 150 pencils and 725 pens. The ratio of the number of pencils to the number of pens in container B is 2 to 3. If all the pencils and pens in container B are placed in container A, then the ratio of the number of pencils to the number of pens in container A would be 3 to 5. What is the total number of pencils and pens in both container A and container B?

A) 5,600
B) 6,725
C) 7,125
D) 7,275
E) 8,000

Answer 1

Option E) 8000

Explanation:

It is given in the question that the number of pencils and pens in a container A are 150 and 725.

Let the number of pens and pencils in container B are x and y.

As per statement " Ratio of the number of pencils to the number of pens is 2:3"

Equation will be
`(x)/(y)=(2)/(3)`

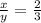
Or
`x=(2)/(3)y`------(1)

Second statement says "If all pens and pencils of container B are placed in container A then ratio of pencils and pens would be 3:5"

Equation will be
`(x+150)/(y+725)=(3)/(5)`

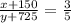
5(x + 150) = 3(y + 725) [By cross multiplication]

5x + 750 = 3y + 2175

5x - 3y = 2175 - 750

5x - 3y = 1425 ------(2)

Now we put
`x=(2)/(3)y`

`5((2y)/(3))-3y=1425`

`(10y)/(3)-3y=1425`

`(10y-9y)/(3)=1425`

`(y)/(3)=1425`

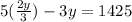
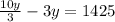
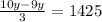
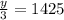
y = 3×1425

y = 4275

Now we put y = 4275 in equation 1

`x=(2)/(3)(4275)`

x = 2850

Now (x + y) = 2850 + 4275

= 7125

Now Total number of pen and pencils in container A and container B

= 150 + 725 + 7125

= 8000

Therefore, Option E) is the answer