Answer:
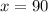
Explanation:
The first step is to substitute $6700 in the position of C(X) in the formula:

To solve the second-degree equation use the formula:
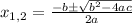
Where
 is the coefficient of the
is the coefficient of the
 (
(
 ),
),
 is the coefficient of the
is the coefficient of the
 (
(
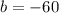 ) and
) and
 is the constant part (
is the constant part (
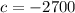 )
)

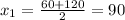
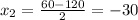
The number of units manufactures is 90. The other value of x doesn't make sense in the contest of the problem.