Question

The annual increase in height of cedar trees is believed to be distributed uniformly between five and ten inches. Find the probability that a randomly selected cedar tree will grow less than 8 inches in a given year. Round your answer to four decimal places, if necessary.

Answer 1

1(1/7) or 0.1428

Explanation:

To find the probability of a randomly selected ceder tree that will grow less than 8 inches in a given year is,

lets Recall that Area= Width x Height

The number 12 is declared as a given year (1 year)

Therefore

The height= 1/12-5= 1/7

The width= 6-5=1

For area= 1(1/7)

1(1/7)=0.1428

Answer 2

Answer: 0.6000

Explanation:

Given : The annual increase in height of cedar trees is believed to be distributed uniformly between 5 and 10 inches.

Then the probability density function:-

`f(x)=(1)/(10-5)=(1)/(5)`

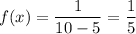
Then , the probability that a randomly selected cedar tree will grow less than 8 inches in a given year will be :-

`P(x\leq8)=\int^8_5f(x)\ dx\\\\=\int^8_5((1)/(5))\ dx\\\\=(1)/(5)[x]^8_5\\\\=(1)/(5)*(8-5)=(3)/(5)=0.6000`

Hence, the probability that a randomly selected cedar tree will grow less than 8 inches in a given year =0.6000