Question

Microwaves of wavelength 4.60 cm enter a long, narrow window in a building that is otherwise essentially opaque to the incoming waves. If the window is 34.5 cm wide, what is the distance from the central maximum to the first-order minimum along a wall 6.35 m from the window?

Answer 1

The distance from the central maximum is 0.854 m.

Step-by-step explanation:

Given that,

Wave length = 4.60 cm

Width d= 34.5 cm

Distance L= 6.35 m

We need to calculate the angle

Using relation width and wavelength

`d\sin\theta=n\lambda`

`\sin\theta=(n\lambda)/(d)`

`\theta=\sin^(-1)(n\lambda)/(d)`

`\theta=sin^(-1)(4.60)/(34.5)`

`\theta=7.66^(\circ)`

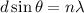
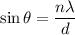
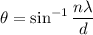
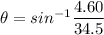
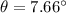
We need to calculate the distance from the central maximum

`y=L\tan\theta`

`y=6.35*\tan7.66`

`y=0.854\ m`

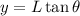
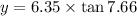
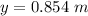
Hence, The distance from the central maximum is 0.854 m.