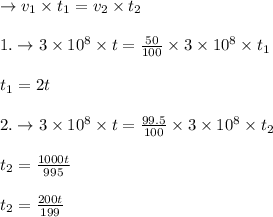Answer with explanation:
Relation between Speed , Distance and time
Distance =Speed × Time
→It means Speed is inversely Proportional to time.
As distance will remain constant , in that frame of reference
If speed of light in a Medium
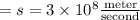
Then, time taken to cross the medium = t seconds or hours or another unit of time.
Now, If speed of light is 50% of the speed of light relative to us
That is Speed of light in another medium

Then, time taken to cross the medium = 2t seconds or hours or another unit of time.
Using Unitary Method