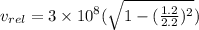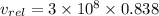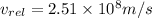Question

A law enforcement officer in an intergalactic "police car" turns on a red flashing light and sees it generate a flash every 1.2 s. A person on earth measures that the time between flashes is 2.2 s. How fast is the "police car" moving relative to the earth?

Answer 1

The velocity of the police car relative to earth is
`v_(rel) = 2.51* 10^(8) m/s`

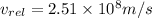
Given:

time for flash generation of the inter galactic police car, t = 1.2 s

time between flashes as measured from earth, t' = 2.2 s

Solution:

Utilising Einstein's equation for time dilation to calculate the velocity of the police car, the equation is given by:

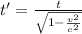`t' = \frac{t}{\sqrt {1 - (v^(2))/(c^(2))}}` (1)

where, c = speed of light in vacuum =
`c = 3* 10^(8)`

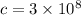
re arranging eqn (1) for velocity, v:

`v_(rel) = c* \sqrt {1 - ((t)/(t'))^(2)}` (2)

Now, from eqn (2)

`v_(rel) = 3* 10^(8)( \sqrt {1 - ((1.2)/(2.2))^(2)})`

`v_(rel) = 3* 10^(8)* 0.838`

`v_(rel) = 2.51* 10^(8) m/s`