Question

When the polynomial 3x^3+4x^2+kx+4 is divided by 3x-5 the remainder is 39. Find the value of k and the quotient.

Answer 1

k = 6

Explanation:

According to factor/remainder theorem, we will take the value of x which makes 3x-5 equal to 0 and put it into the polynomial and equate it to the remainder.

3x - 5 = 0

3x = 5

x = 5/3

Putting into polynomial:

`3((5)/(3))^3+4((5)/(3))^2+k((5)/(3))+4=39\\3((125)/(27))+4((25)/(9))+(5)/(3)k=35\\(125)/(9)+(100)/(9)+(5)/(3)k=35\\(225)/(9)+(5)/(3)k=35\\(5)/(3)k=10\\k=6`

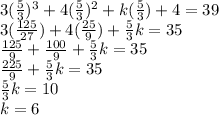
The value of k is 6