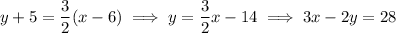1a. Use the Pythagoren theorem:
AC^2 = 7.2^2 + 9.6^2 ==> AC = 12
1b. Same as in (1a), but now use AC as the length of another leg, and AG would be the hypotenuse in triangle ACG:
AG^2 = AC^2 + 3.5^2 ==> AG = 12.5
1c. This requires some trigonometry. In the triangle ACG, we have two legs of length AC = 12 and CG = AE = 3.5. Then the angle
 made by AG with the floor, which is the same as the angle made by AG and AC, is such that
made by AG with the floor, which is the same as the angle made by AG and AC, is such that
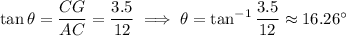
2a. (6, -5) is not on the line because
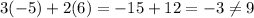
2b. Gradient is another word for slope. Here we can rewrite the line as
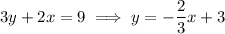
which tells us the slope is -2/3.
2c(i). Any line perpendicular to L has a slope equal to the negative reciprocal of the slope of L. Here, that would be 3/2.
2c(ii). Using the point-slope formula, this perpendicular line has equation