Answer:
Initial amount of the element taken was 224 grams.
Explanation:
Half life of the element AoPSium is 120 years.
We know the radioactive decay is represented by the formula

where A(t) = Element remaining after time t
A(0) = Initial amount
t = time in years
k = decay constant
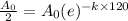
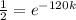
Now we take natural log on both the sides of the equation
![ln((1)/(2))=ln[(e)^(-120k)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/ymcxf4uxe9gju1gv7jj21c2co22o2ctp9s.png)
-0.69314 = - 120k
k =
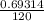
k = 0.005776
Now we have to calculate the amount taken of the element after 600 years when amount remaining was 7 grams.

7 =
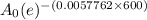
7 =
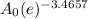
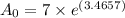
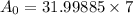
 grams
grams
Therefore, Initial amount of the element taken was 224 grams.