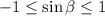Answer:
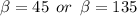
Explanation:
We want to solve
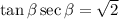 , where
, where
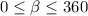 .
.
We rewrite in terms of sine and cosine.
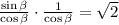
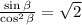
Use the Pythagorean identity:
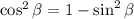 .
.
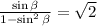
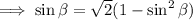
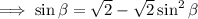
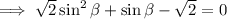
This is a quadratic equation in
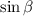 .
.
By the quadratic formula, we have:
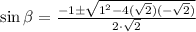
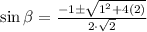
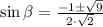
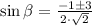
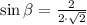 or
or
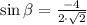
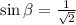 or
or
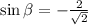
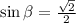 or
or
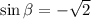
When
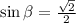 ,
,
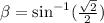
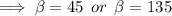 on the interval
on the interval
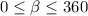 .
.
When
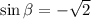 ,
,
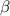 is not defined because
is not defined because