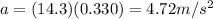Question

FIGURE 2 shows a constant force, F of magnitude 20N pulled a light cord wrapped around a pulley to lift a bucket of mass 1.53kg. The radius and the moment of inertia of the pulley are 0.330m and 0.385kg m² respectively. If the frictional torque is 1.10Nm calculate the

(a) angular acceleration of the pulley. (b) linear acceleration of the bucket​

Answer 1

(a)
`14.3 rad/s^2`

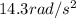
The angular acceleration of the pulley can be found by using the equivalent of Newton's second law for rotational motions:

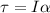`\tau = I \alpha` (1)

where

`\tau` is the net torque on the pulley

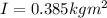`I=0.385 kg m^2` is the moment of inertia of the pulley

`\alpha` is the angular acceleration

First, we need to find the net torque. The torque exerted by the force F (forward) is:

`\tau_t = F r = (20 N)(0.330 m)=6.6 Nm`

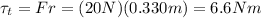
While the frictional torque (backward) is
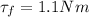`\tau_f = 1.1 Nm`. So, the net torque is

`\tau = \tau_t - \tau_f=6.6 - 1.1 = 5.5 Nm`

Now, re-arranging eq.(1), we find the angular acceleration:

`\alpha = (\tau)/(I)=(5.5)/(0.385)=14.3 rad/s^2`

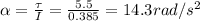
(b)
`4.72 m/s^2`

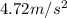
Assuming that the string holding the bucket is inextensible, the bucket should have the same linear acceleration of a point on the edge of the pulley, which is given by

`a= \alpha r`

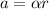
where

`\alpha=14.3 rad/s^2` is the angular acceleration

r = 0.330 m is the radius of the pulley (the distance of a point at the edge from the centre)

Substituting into the equation, we find

`a=(14.3)(0.330)=4.72 m/s^2`