Question

Consider a population whose growth over a given time period can be described by the exponential model: dN/dt = rN. Select the correct statement about this population.a. A population with an r of 0.1 will decrease over time.b. A population with an r of 0 will have no births or deaths during the time period under consideration.c. A population with a positive value of r will grow exponentially.

Answer 1

b and c

Explanation:

We are given that a population whose growth over a given time period can be described by the exponential model

`(dN)/(dt)=r N`

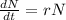
Let initial population =
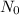`N_0` when time t=0

`\int(dN)/(N)=r\int_0^tdt`

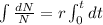
After integrating

We get ln N=rt +C

Where C is integration constant

When t=0 then N=
`N_0`

`ln N_0=C`

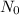
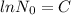
Substitute the value of C then we get

`ln N=rt +ln N_0`

`ln N-ln N_0=rt`

`ln(N)/(N_0)=rt`

`(N)/(N_0)=e^(rt)`

`N=N_0e^(rt)`

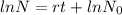
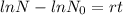
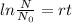
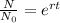
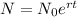
When r=0.1 then we get

`N=N_0e^(0.1t)`

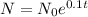
Hence, the population increase not decrease.

When r= 0

Then we get

`N=N_0e^(0)`

`N=N_0`

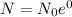
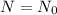
Hence, the population do not increase or decrease.

So, a population with r of 0 will have no births or deaths during the time period under consideration.

If we take a positive value of r then the population will increase exponentially .

Hence, option b and c are both correct.