Question

X and Y work at constant rates. How many more hours does it take machine Y, alone, to fill an order of a certain size than machine X alone? I. X and Y together fill order in 2⁄3 the time that X alone does. II. Y alone does it in twice the time as X alone does.

Answer 1

Answer with explanation:

V=Volume of tank

It is given that, X and Y work at constant rates.

Let rate of doing work of X is x hour.

And, Rate of Doing work of Y is y hour.

Statement I----X and Y together fill order in 2⁄3 the time that X alone does.

`(V)/(x+y)=(2V)/(3x)\\\\x+y=(3x)/(2)\\\\y=(x)/(2)`

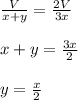
-------------------------------------------------(1)

Statement II----Y alone does it in twice the time as X alone does.

`(V)/(x)=(V)/((y)/(2))\\\\y=(2)/(x)`

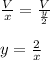
Substituting the value of y in 1

`\rightarrow (x)/(2)=(2)/(x)\\\\\rightarrow x^2=4\\\\\rightarrow x=\pm 2\\\\\rightarrow x=2`

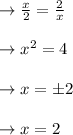
→x≠ -2, because Rate of doing work can't be negative.

Substituting the value of x in 1, gives

`y=(2)/(2)\\\\y=1`

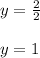
→Rate of doing work of X= 2 hour

→Rate of doing work of Y=1 hour