Question

2 taps A and B can fill a swimming pool in 3 hours. If turned on alone, it takes tap A 5 hours less than tap B to fill the same pool. How many hours does it take tap A to fill the pool?

Answer 1

Tap A will take 2 hours and tap B will take 6 hours to fill the tank when turned on alone.

Explanation:

Let tap B fills the pool alone in the time = x hours

So in one hour part of pool will be filled =
`(1)/(x)`

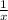
Another tap A when turned on, it takes time to fill the pool = x-5 hours

So in one hour part of the same pool filled =
`(1)/(x-5)`

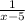
Now both the taps A and B are turned on then time taken to fill the pool = 3 hours.

Part of the pool filled in one hour by both the taps =
`(1)/(3)`

Now we form an equation

Part of pool filled in one hour by tap A + Part of pool filled in one hour by tap B = Part of pool filled in one hour by both the taps when turned on

`(1)/((x-5))+(1)/(x)=(1)/(3)`

`(x-5+1)/(x(x-5))=(1)/(3)`

`(x-4)/(x(x-5))=(1)/(3)`

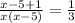
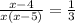
3(x - 4) = x(x - 5)

x² -5x = 3x - 12

x² - 8x + 12 = 0

x² - 6x - 2x + 12 = 0

x(x - 6) - 2(x - 6) = 0

(x -2)(x - 6) = 0

x = 2, 6 hours

We will take higher value of x as x = 6 hours for tap B.

Time taken by tap A = 6 - 4 = 2 hours.

Therefore, Tap A will take 2 hours and tap B will take 6 hours to fill the tank when turned on alone.