Question

A square and an equilateral triangle have equal perimeters. The area of the triangle is $2\sqrt {3}$ square inches. What is the number of inches in the length of the diagonal of the square?

Answer 1

An equilateral triangle with side length
`x` has area
`\frac{\sqrt3}4x^2`, so that

`\frac{\sqrt3}4x^2=2\sqrt3\implies x^2=8\implies x=2\sqrt2`

Then the triangle, and hence the square, has a perimeter of
`3x=6\sqrt2`.

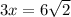The perimeter of a square with side length
`y` is
`4y`, so that

`4y=6\sqrt2\implies y=\frac{3\sqrt2}2`

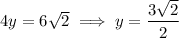
The length of the diagonal of any square is
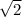`\sqrt2` longer than the length of its side, so that this square's diagonal length is

`\sqrt2\,y=\frac{3(\sqrt2)^2}2=\boxed{3}`