Question

A(n) 636 kg elevator starts from rest. It moves upward for 4.5 s with a constant acceleration until it reaches its cruising speed of 2.05 m/s. The acceleration of gravity is 9.8 m/s 2 . Find the average power delivered by the elevator motor during this period. Answer in units of kW.

Answer 1

The average power delivered by the elevator motor during this period is 6.686 kW.

Step-by-step explanation:

Given;

mass of the elevator, m = 636 kg

initial speed of the elevator, u = 0

time of motion, t = 4.5 s

final speed of the elevator, v = 2.05 m/s

The upward force of the elevator is calculated as;

F = m(a + g)

where;

m is mass of the elevator

a is the constant acceleration of the elevator

g is acceleration due to gravity = 9.8 m/s²

`a = (v-u)/(t) \\\\a = (2.05 -0)/(4.5) \\\\a = 0.456 \ m/s^2`

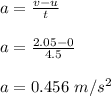
F = (636)(0.456 + 9.8)

F = (636)(10.256)

F = 6522.816 N

The average power delivered by the elevator is calculated as;

`P_(avg) = (1)/(2) (Fv)\\\\P_(avg) = (1)/(2) (6522.816 \ * \ 2.05)\\\\P_(avg) = 6685.89 \ W\\\\P_(avg) = 6.68589 \ kW\\\\P_(avg) = 6.686 \ k W`

Therefore, the average power delivered by the elevator motor during this period is 6.686 kW.