Question

The age of a piece of wood from an archeological site is to be determined using the Carbon-14 method. The activity of the sample is measured to be 0.596 times the Carbon-14 activity of living plants. What is the age of the sample in years? (The half-life of the Carbon-14 isotope is 5730 years.)

Answer 1

4276.98 years

Step-by-step explanation:

t = age of the sample in numbers of years

T = half life of the carbon-14 isotope = 5730 yrs

λ = decay constant of carbon-14

decay constant is given as

`\lambda =(0.693)/(T)`

`\lambda =(0.693)/(5730)`

`\lambda = 0.000121`

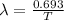
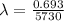
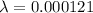
A₀ = activity of Carbon-14 in living plants

A = activity of Carbon-14 after time "t" = (0.596) A₀

Using the equation

`A = A_(o) e^(-\lambda t)`

`(0.596) A₀  = A_(o) e^(-0.000121 t)`

`0.596 = e^(-0.000121 t)`

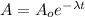
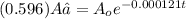
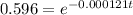
t = 4276.98 years