Question

Jason paddled his canoe 24 miles upstream for 4 hours. It took him 3 hours to paddle back. Find the speed of the canoe in still water and the speed of the river current.

Answer 1

Speed of the canoe in still water is 7 miles per hour and speed of the river stream will be 1 miles per hour.

Explanation:

Let the speed of canoe paddled by Jason in still water is x miles per hour and speed of the river current y miles per hours.

As per statement of the question,

Resultant speed of canoe upstream = (x - y)

and speed of canoe with the stream = (x + y)

Now as per statement,

`(x - y)=(24)/(4)`

x - y = 6 ------(1)

and
`(x + y)=(24)/(3)`

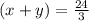
x + y = 8 ------(2)

Now we add equation 1 and 2.

(x - y) + (x + y) = 6 + 8

2x = 14

x = 7

By putting x = 7 in equation 2

7 + y = 8

y = 8 - 7

y = 1

Therefore, Speed of the canoe in still water is 7 miles per hour and speed of the river stream will be 1 miles per hour.