Question

Use the functions f(x) and g(x) to determine which function has the largest zero and provide its coordinates. f(x) = 4x2 − 16x + 16

x g(x)
18 −17
19 0
20 19
21 40
22 63

f(x); (−2, 0)
f(x); (2, 0)
g(x); (19, 0)
g(x); (63, 0)

Answer 1

g(x); (19,0)

Explanation:

The zeros are the x values where the graph intersects the x-axis. To find zeros replace y with 0 and solve for x.

f(x) = (2,0)

Answer 2

The function that has the largest zero is g(x) and its coordinates are (19,0)

Explanation:

we know that

The zeros of the function (or x-intercepts) are the values of x when the value of the function is equal to zero

we have

`f(x)=4x^(2)-16x+16`

Find the x-intercepts of f(x)

Equate f(x) to zero

`4x^(2)-16x+16=0`

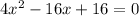
Complete the square

`4(x^(2)-4x)=-16`

`4(x^(2)-4x+4)=-16+16`

`4(x^(2)-4x+4)=0`

`4(x-2)^(2)=0`

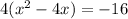
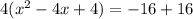
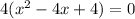
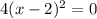
`x=2` -----root with a multiplicity of 2

therefore

The x-intercept of f(x) is the point (2,0)

Find the x-intercept of g(x)

Observing the table

For g(x)=0, x=19

therefore

The x-intercept of g(x) is the point (19,0)

Compare the zeros of f(x) and g(x)

The function that has the largest zero is g(x) and its coordinates are (19,0)