Answer:
The difference between the maximum value of g(x) and the minimum value of f(x) is:
5
Explanation:
- The function f(x) is given by:
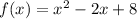
which in vertex form is given by:
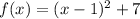
Now, we know that:
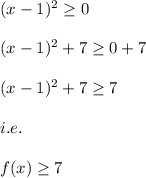
Hence, the minimum value of the function f(x) is: 7
- Also, the function g(x) is a parabola that opens down and passes through (0,3) , (3,12) and (5,8) .
Let the equation for g(x) be:

Now with the help of the passing through three points we get:
when it passes through (0,3)
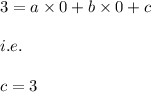
when it pass through (3,12)
i.e.
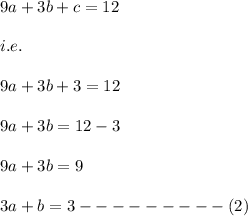
Also it pass through (5,8)
i.e.
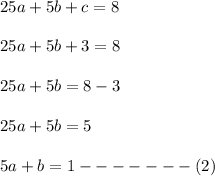
On subtracting equation (2) from equation (1) we have:

and by putting the value of a in equation (1) we have:
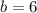
Hence, we get:
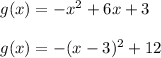
Now, we know that:
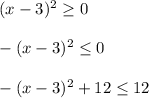
This means that the maximum value of g(x) is: 12
The difference between the maximum value of g(x) and the minimum value of f(x) is:
12-7=5