Answer:
Center (0,0)
Vertices (-15,0), (15,0), (0,-25), (0,25)
Foce (0,-20), (0,20)
Explanation:
You are given the ellipse equation
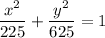
The canonical equation of ellipse with center at (0,0) is
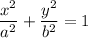
So,
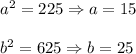
Hence, the center of your ellipse is at (0,0) and the vertices are at points (-15,0), (15,0), (0,-25) and (0,25)
This ellipse is strengthen in y-axis, so
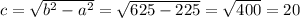
and the foci are at points (0,-20) and (0,20).