Answer:
Problem:
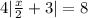 .
.
Solution given:

The other solution:
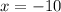
Step-by-step explanation:
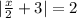
Means the value inside the absolute value has to be 2 or -2 since |2|=2 and |-2|=2.
So you already have
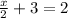 .
.
You need that
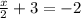 .
.
Let's solve this equation:
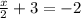
Subtract 3 on both sides:
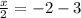
Simplify:
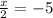
Multiply both sides by 2:

Simplify:
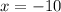
So x=-2 or x=-10.
Checking!
x=-2:
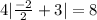
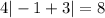
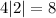
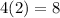
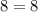 is true so x=-2 checks out.
is true so x=-2 checks out.
x=-10:
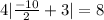

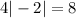
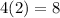
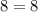 is true x=-10 checks out.
is true x=-10 checks out.
It has been confirmed that -2 and -10 satisfy the equation:
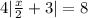 .
.