Answer:
110
Explanation:
There is a theorem that says "The measure of an angle formed by a secant and a tangent drawn from a point outside the circle is HALF the difference of the intercepted arcs "
Hence we can say:
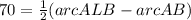
We can say:
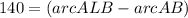
Also, we know that circle's degree measure is 360, thus we can say:
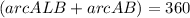
To find Arc AB, we can use the two equations and add, thus we get:
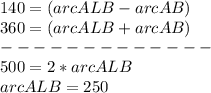
Thus, arc AB = 360 - 250 = 110
2nd answer choice is right.