Answer:
d. 4x+3y≤12
Explanation:
To solve the problem we need to find the equation of the red line, since it is part of the inequality.
This should be like the following y=mx+b, where 'm' is the slope.
The slope can be obtained using the following equation:
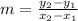
If we use the points given by the graph (0,4) and (3,0) we will obtain that m=-4/3
Now, to find 'b' we just need to evaluate any point ine equation y=mx+b. iike (0,4).
4=-4/3*0 + b.
b=4
Our line has the following equation: y= -(4/3)*x +4, that can be written in standard form as 3y+4x=12
The region is below the graph, hence our inequality shoul be 3y+4x<=12.
The iqual sign part comes watching the graph, the line is drawn using solid line, hence the line is included in the region.