Hello! Your answer is B, 10 minutes.
Say the x = minutes taken to do the job. You can set up an equation like this to solve this.
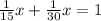
This is representative of the situation. The fractions each represent how much each person does in a minute, and when they're multiplied by x, that's how much of the project they get done based off of the minutes they work together on the job. Add the two together, and you get how much of the project is finished in x amount of time. Set it equal to 1, as you are looking for 100% completion.
Once you have this equation, find a common denominator, add, and solve.
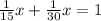
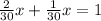
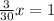
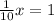
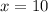
Therefore, it will take them 10 minutes to do the job together.
Hope this helps!