Answer:
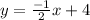
Explanation:
First we need to find the slope of the given line, the one that is passing trough the points (-4,0) and (4,-4).
For that, lets use the slope`s equation

m= (-4-0) / (4-(-4)) = -1/2
A line that is parallel to this one must have its same slope, so m2= -1/2
Now, lets find the 'y' axis intercept point using the point given: (2,3)
And the equation for lines: y=mx+b
By evaluating (2,3) in the above expression we have:
3=-1/2 * 2 +b
From here, we obtain that b=4
Hence, our line is y=-1/2 * x + 4