Question

Please help me with this question

Answer 1

Opt. 4: Tan(15)=tan(30/2)= +/- sqrt(1-cos30) / sqrt(1+cos(30))

Explanation:

To solve this identity is a key objective to remind the following expression:

(sin(x/2))^2= 1 - (cos(x/2))^2 (a)

The following to remember is this:

cos(x)=cos(x/2 + x/2)= (cos(x/2))^2 - (sin(x/2))^2 (b)

Lets substitute equation (a) in (b)

we have (cos(x/2))^2= (1+cos(x))/2

Lets apply square root to both sides of equality sign:

sqrt((cos(x/2))^2= (1+cos(x))/2)

cos(x/2)= sqrt( (1+cos(x))/2 ) (c)

Use (c) in (a)

(sin(x/2))^2 = 1 - (1 + cos(x)) /2

Lets apply square root to both sides of equality sign:

sqrt((sin(x/2))^2 = 1 - (1 + cos(x)) /2)

We obtain that:

sin(x/2)= sqrt (1-cos(x) ) /2 ) (d)

Finally tan(x/2) is equation (d) divided by equation (c)

`tan(x/2) = \sqrt{(1-cos(x))/(1+cos(x))}`

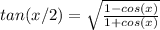
Just need to evaluate x=30.

The signs +/- comes out sinces there is a square root involved and you can have either a positive answer or a negative.