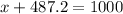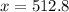Answer:
512.8 + 487.2
Explanation:
Let the two numbers be x and y respectively. The sum of x and y is 1000:
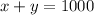
The difference between their squares is 25600:
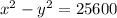
We two unknowns(x and y) and two equations and therefore we can solve for x or y:
Lets:
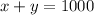
and
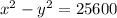
We can simplify the expression as:

We can substitute x+y=1000 into this expression:
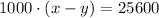
We can now write x in terms of y and vice verse, therefore:
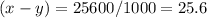
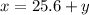
We have simple expression and can substitute it into x+y=1000
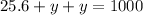
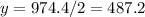
therefore x can be solved by using the value of y and substituting it into x+y=1000: