A 15.5 kg block is pulled by two forces. The first is 11.8 N at a 53.7 angle and the second is 22.9 at a -15.8 angle. What is the magnitude and direction of the acceleration?

Question

asked Aug 16, 2020 374 views

2 Answers

Kahler · Answer 1 · 2020-08-23T03:07:41+0000

Answer:

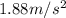1.88 m/s^2 at
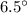
$6.5^(\circ)$

Step-by-step explanation:

We need to calculate the components of the resultant force on both the x (horizontal) and y (vertical) direction.

Components of the first force F1:

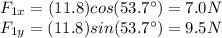
$F_(1x) =(11.8) cos (53.7^(\circ))=7.0 N\\F_(1y) = (11.8) sin (53.7^(\circ))=9.5 N$

Components of the second force F2:

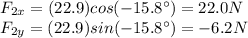
$F_(2x) =(22.9) cos (-15.8^(\circ))=22.0 N\\F_(2y) = (22.9) sin (-15.8^(\circ))=-6.2 N$

So the components of the resultant force are

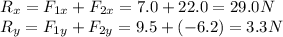
$R_x = F_(1x)+F_(2x)=7.0+22.0 = 29.0 N\\R_y = F_(1y)+F_(2y) = 9.5+(-6.2)=3.3 N$

So the magnitude of the resultant force is

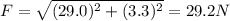
F=√((29.0)^2+(3.3)^2)=29.2 N

And the direction is

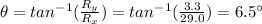
$\theta = tan^(-1) ((R_y)/(R_x))=tan^(-1) ((3.3)/(29.0))=6.5^(\circ)$

The magnitude of the acceleration can be found by using Newton's second law:

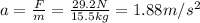
a=(F)/(m)=(29.2 N)/(15.5 kg)=1.88 m/s^2

while the direction is the same as the resultant force,
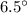$6.5^(\circ)$ .