Question

Can somebody prove this mathmatical induction?

Answer 1

See explanation

Explanation:

1 step:

n=1, then

`\sum \limits_(j=1)^1 2^j=2^1=2\\ \\2(2^1-1)=2(2-1)=2\cdot 1=2`

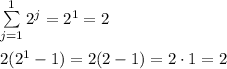
So, for j=1 this statement is true

2 step:

Assume that for n=k the following statement is true

`\sum \limits_(j=1)^k2^j=2(2^k-1)`

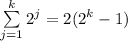
3 step:

Check for n=k+1 whether the statement

`\sum \limits_(j=1)^(k+1)2^j=2(2^(k+1)-1)`

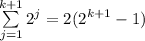
is true.

Start with the left side:

`\sum \limits _(j=1)^(k+1)2^j=\sum \limits _(j=1)^k2^j+2^(k+1)\ \ (\ast)`

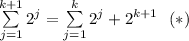
According to the 2nd step,

`\sum \limits_(j=1)^k2^j=2(2^k-1)`

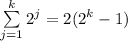
Substitute it into the
`\ast`

`\sum \limits _(j=1)^(k+1)2^j=\sum \limits _(j=1)^k2^j+2^(k+1)=2(2^k-1)+2^(k+1)=2^(k+1)-2+2^(k+1)=2\cdot 2^(k+1)-2=2^(k+2)-2=2(2^(k+1)-1)`

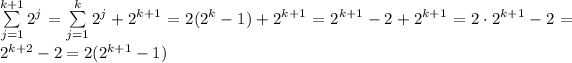
So, you have proved the initial statement