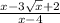Answer:
8b) 2x+
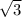 x
x
8c)
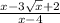
Explanation:
8b)
Multiply the top and bottom by 2+
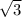 to rationalize this fraction
to rationalize this fraction
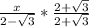
Simplify the product
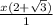
Distribute x through the parenthesis
2x+
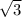 x
x
8c)
Multiply the top and bottom by
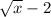 to rationalize this fraction
to rationalize this fraction
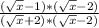
Simplify the product
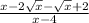
Collect like terms