Question

Two coils close to each other have a mutual inductance of 32 mH. If the current in one coil decays according to I=I0e−αt, where I0=5.0A and α=2.0×103s−1, what is the emf induced in the second coil immediately after the current starts to decay? At t=1.0×10−3s?

Answer 1

The emf induced in the second coil is given by:

V = -M(di/dt)

V = emf, M = mutual indutance, di/dt = change of current in the first coil over time

The current in the first coil is given by:

i = i₀
`e^(-at)`

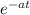
i₀ = 5.0A, a = 2.0×10³s⁻¹

i = 5.0e^(-2.0×10³t)

Calculate di/dt by differentiating i with respect to t.

di/dt = -1.0×10⁴e^(-2.0×10³t)

Calculate a general formula for V. Givens:

M = 32×10⁻³H, di/dt = -1.0×10⁴e^(-2.0×10³t)

Plug in and solve for V:

V = -32×10⁻³(-1.0×10⁴e^(-2.0×10³t))

V = 320e^(-2.0×10³t)

We want to find the induced emf right after the current starts to decay. Plug in t = 0s:

V = 320e^(-2.0×10³(0))

V = 320e^0

V = 320 volts

We want to find the induced emf at t = 1.0×10⁻³s:

V = 320e^(-2.0×10³(1.0×10⁻³))

V = 43 volts