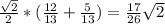Question

Please help with this question

Answer 1

cos(x=pi/4)=
`(17)/(26)*√(2)`

Explanation:

Remember that
`sin^(2)(x) +cos^(2)(x)=1`

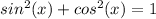
We need to find cos(x) from the above equation.

cos(x)= 12) / 13. This solution is positive since cos(x) in the range (2pi/3, 2pi) is positive.

Now, to obtain cos(x+pi/4) lets use the relation for cos(a+b)= cos(a)*cos(b)-sin(a)*sin(b)

where a=x, b =pi/4

Hence

cos(x+pi/4) =cos(x)*cos(pi/4) - sin(x)*sin(pi/4)

cos(x+pi/4) =
`(√(2))/(2) * (cos(x)+5/13)`

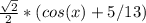
cos(x=pi/4)=
`(√(2) )/(2) *((12)/(13)+(5)/(13))=(17)/(26) √(2)`