Question

Electrons are accelerated through a voltage difference of 230 kV inside a high voltage accelerator tube. What is the final kinetic energy of the electrons? Tries 0/20 What is the speed of these electrons in terms of the speed of the light? (Remember that the electrons will be relativistic.)

Answer 1

kinetic energy is 3.68 ×
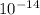`10^(-14)` J

speed of these electrons is 0.5565 c

Step-by-step explanation:

Given data

voltage difference = 230 kV

to find out

kinetic energy and speed of these electrons

solution

we know kinetic energy formula that is

kinetic energy = qv

kinetic energy = 1.6 ×
`10^(-19)` × 230 ×
`10^(3)`

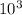
kinetic energy = 3.68 ×
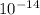`10^(-14)` J

and

speed of electron that is

kinetic energy = m1c² - m2 c²

here m1 = m / √(1-v/c)²

so

KE/mc² = ( 1 / √(1-(v/c)² ) - 1

put value here

3.68 ×
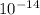`10^(-14)` / (3× 10^8)²×9.11×
`10^(-31)` = ( 1 / √(1-v/c)² ) - 1

0.448835223 = ( 1 / √(1-(v/c)² ) - 1

( 1 / √(1-(v/c)² ) = 0.448835223 + 1 = 1.448835223

√(1-(v/c)² = 1 / 1.448835223 = 0.6902096

(v/c)² = 1 - 0.6902096 = 0.309790

v = 0.5565 c

speed of these electrons is 0.5565 c